ELCAS・最先端科学の体験型学習講座（京都大学理学部）未来の科学者養成講座

2008年9月6日(土)　今井憲一教授

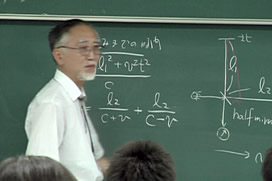で、これとこれと二つ見るとですね、磁場が変化するので■■。当然、電導の時間の関数だと、電場も変化するわけだから、また磁場が発生する。こういう、何度も何度も入れ子になりますよね。で、サインという、サイン、コサインって知ってます？　習いましたか。習ってない？　とにかく、これが変化すればこれができて、これが変化すればこれができる。こういうのを「振動」っていうわけですね。

関数で書くとsinωtという、あるいはコサインでも何でもいいんですけど、三角関数。こういう波を表す関数が、電場と磁場のこういう波が、当然この両方を満たすためにはこういうのが方程式の解として存在するということに直ちに気がついたわけですね。

あるいはこういう必項が必要だということを知って、知った途端に、電磁波というのが存在する。要するに、電場と磁場がこういう格好をしているのがあるよということが、理論的に分かったわけです。 　そうすると、当時の常識としては、波っていうのは、海の波でも音の波でもそうですけど、何か媒質が要るわけですね。海だったら、水がないと波が出ないわけですね。音も空気が振動するから伝わるんで。で、この電磁波が存在するとすると、何か媒質が必要であると。それをエーテルと呼んだわけですね。

何かそういう、波を伝える、電磁波を伝える媒質があるはずである。われわれの周りになければ、電磁波なんていうのは伝わらないだろうと。 　もう一つ彼のやったことは、この方程式を見てみると、波動方程式っていうのがさっと書けるわけですけれど、その速さというのが、光の速さと同じだったんです。

当時、もう光の速度っていうのはある程度の精度で測られてまして、それと同じであるということが気がついたんですね。ですから、光は電磁波に違いないという結論を出すわけです。これは、理論的に求めた電磁波の速度と実験的に求めた光の速度が同じだったということから、そういう結論を得ます。 　

ヘルツの実験

それで、次に現われたのが、このヘルツっていう人ですね。ヘルツって知ってますよね。周波数の単位になってます。マクスウェルっていうのは偉い人なんですけど、さっき言った電磁気学を完成させた人なわけですけど、単位にはなってないです。長いんですね、名前がね。マクスウェルっていう。ヘルツは短いので、周波数の単位になってます。この人はドイツの物理学者で、どこだったかな、大学忘れました。この人のやったことは、電磁波の確認。「ヘルツの実験」という有名な実験があります。あるところの火花放電をさせて、周りに電場がどうできるかっていうのを測定してみた。そうすると、なるほど、電磁波が測定されたというわけです。

観測に成功しました。これはちょっと時間かかってますね。1864年にそれがあるはずだといって、確認したのにはかなりかかってますけど、これが確認されたら、たちまち無線通信で、タイタニック号が沈没したときにはもう無線が生まれていました。現代、テレビやラジオや携帯がない世界っていうのは多分信じられないでしょうけど、その電磁波っていうのがマクスウェルとヘルツによって発見され、使われるようになったというわけです。 　それで、もう一つ重要なことは、ヘルツのやったことはですね、「ヘルツの方程式」というのを作ったんですね。それはですね、こういうことです。今、座標変換ということをいうんですけど、慣性系座標変換。これは、電車がですね、何か走ってる。速度ｖで走ってるとしましょう。それで、ここで人が見てると。ね。この二つを慣性系といいます。こういう座標があるとしますと、ｚ、ｘ、ｙ。こっちはｚ、こっちをｙとつけましょうね。ｘ、ｙ。

こういう関係を今、考えてくださいね。地上に静止した人と、走ってる電車。一定の速度で走ってる電車。こういう座標の変換を、座標変換、慣性系の座標変換といいます。慣性系っていうのは、一定の速さで走ってるということですね。 　それで、古典物理学、古典の力学ですね。ニュートンの力学では、ｘはx´＋vtと書けます。要するに、ベロシティーで一定で、ｖで走ってるわけですから、ｘで測った距離と、ここを例えば原点だとしますと原点０ですけど、ｘの点はずーっと動いていきますから、vtで書けますよね。ニュートンの運動方程式は、こういうニュートンの運動方程式ってありますよね。Ｆイコール、有名な力と加速度の。これがすべて、古典力学のすべてなんですよね。大砲の弾が打ったらどう動くかとか、地球が月の周りを、地球の周りを月はどう運動するかとか、そういう運動はすべてこの式で書けるわけですが、この方程式は、この座標変換をしても変わらないんですね。要するに、この慣性系で見て、この電車に乗っても止まっても、どっちから見てもこの式は同じように書けるんです。

だから、この変換、こういう式が普通の常識的ですよね。速度。これが走ってれば速度が足し算になるっていう、ただそれだけのことですけれど。 　ところがですね、この電磁気のマクスウェル方程式。電磁気を記述する式は、こういう変換をしてやると、こういう変換をしてあげたわけです。要するに、ここで起こってる電磁現象をここから見たらどう見えますかっていう。ね。ここで、電磁誘導の法則とかクーロンの力とか、なんか測ってる。ここの人がそれを見たらどう見えるか。それをしたのがヘルツ先生のもう一つの業績で、ヘルツの方程式っていうのを作ったんです。

アルバート・マイケルソン　光の速度の精密測定

ところが、実験をしているとどうも合わないと。ね。それが19世紀末の時代です。で、そこで登場するのが、このマイケルソンという人ですね。アメリカ人として初めてノーベル賞をもらった人ですね。アルバート・マイケルソン。この人がやったことは、光の速度の精密測定ということで、「マイケルソン干渉計」っていいますけど、光っていうのは波なので、半波長ずれると、で、足してあげるとこれが消えちゃいますよね。レンズなんかの反射を防止する薄いフィルムについてるのなんか、この原理を応用してるんですけど、要するに、波がずれた■■を足してあげると、強まったり弱まったりします。

その原理を応用して光の速度を測る。要するに、ちょっとずれている。これ、光の波長っていうのはミクロン以下ですから。ミクロン以下ですよね、数百ナノメーター。だから、すごい精度で光の速度を測ることができます。それを発明して、彼は、当然エーテルは存在してると信じてますから、エーテルに対する地球の速度を測ろうとします。 　で、どういうふうに測るかといいますと、地球は太陽の周りをこう回ってますから、エーテルが静止してるとすると、地球の速度、ｖという速度でエーテルに対して運動してることになります。

地球に乗ってみると、今度エーテルが、の風が吹いてることになりますね。で、彼はこういう実験をしました。こことここに鏡を置いて、こちらが東側、これが北側になります。地球のですよ。地球の東と北に向けてある一定の距離に鏡を置いて、それでここに、ハーフミラーというんですけど、半分通して半分反射させるっていうやつですね。で、ここから光を入れてあげるわけです。で、こっちを通ってきたやつを、この干渉計で見ると。これが干渉計なんですね。それで、こっち行って返ってきたやつと北へ行って返ってきたやつをここで干渉させて、それで見る。で、行って返ってきた時間、東へ行って返ってきた時間と北へ行って返ってきた時間は、当然、これは東に向かって運動してるわけですから、違うだろうと。ね。この系はｖで走ってるわけですね、ブイーンって。だから、こっち行った時間とこっち行った時間は違う。分かります？　式で書いて■■ね、式で。まあいいか。

僕は、高校生に講義をしたことはほとんどないので、何か分からないことがあったら質問してくださいね。いつでもインタラクトして。質問するのは、自分のためだけじゃなくて、みんなのためだと思ってくださいね。自分が分からないことはみんなも分からないと信じて疑わないほうがいいです。

ちょっと今から式を書きますね。こちらがL1、この距離をL1、この距離をL2としましょう。そうすると、北まで。北の■■までの時間ｔを光速ｃで割りますと、ルートkhの２乗＋ｐの２乗■■となります。いいですか。要するに、これが一定の間にこう動いてるわけですから、実際にはこう反射しても、向こうに行ってますから、こう返ってくるわけですね。だからこういう式になります。

これだけ動いちゃってて、こう行って返ってくる間にこれだけ動いちゃってるわけですから、ｖ２乗の■■という、この距離が（不明）。で、これを往復するんだと、これの２倍ですね。で、東の、東に行った場合はどうなるか。これは時間ですね。東の時間は、ｃ足すｖ分のL2、足す（不明）。要するに、ベースはこうｖで動いてますから、光速は、同じ方向に行くときは足し算になるし、反対に向かうときは引き算になる。これは何となく常識的ですよね。 　そういう式を立てて、それで、Δtという、ｔの東行った時間と北に行った時間というのを計算します。これは簡単な式で計算します。

時間がないので答えだけ言いますと、大体ですね、ｃ分のＬのβの２乗。βというのは、なんかこう出てきますけど、ｃ分のｖですね。この地球の運動してる速度を、光速で割ったもの。というわけで、この時間差を測ると、地球がエーテルに対してどれだけのスピードで走ってるかということが分かりますというわけです。それがマイケルソンの実験です。